
1K20がボーダーの台で、1K22の台を発見して1か月ブン回したのに勝てない!
みたいに、考えている人向けの記事です。
さて、パチンコでは「ボーダーを上回る台を打ち続ければ勝てる」というほど単純ではないです。
パチンコで勝つために必要な壁は、ボーダー以外にもう一つあります。
それが、統計学でいう「信頼区間」という概念。
「信頼区間」を、わかりやすい言葉で言い換えると、「相性」とか「誤差」のこと。
つまりは、「ボーダーを上回る台」かつ「相性のいい台であること」が、勝つために必要になります(*´ω`)。
そもそもボーダー理論とは何かを簡単に説明

そもそもボーダー理論が、わかったようなわからないような。
という人もいると思うので、簡単に説明します。
ボーダー理論とは、ボーダーライン以上の台を打てば勝てる理論のこと
ボーダー理論は、「ボーダーラインが20回転だったら、20回転以上の台を打てば勝てるんじゃね?」的な理論のことです。

ボーダーラインって何?
ボーダーラインとは、プラスマイナスゼロになる回転数の境目のことです。

「ボーダー=border=境目」です!
例えば、1K(1,000円)あたり20回転がボーダーラインだとしたら、
- 20回転回る台に座れば±0
- 19回転回る台に座ればマイナス(単純計算で打つたびに所持金が、19/20に減る)
- 21回転回る台に座ればプラス(単純計算で打つたびに所持金が、21/20に増える)
ということになります。
ボーダー理論についてもう一度言うと「ボーダーラインが20回転だったら、20回転以上の台を打てば勝てるんじゃね?」的な理論のことです。
ボーダーラインの求め方は期待値

それじゃあ、ボーダーラインってどうやって求めるの?
と言われれば、期待値です。
期待値っていうのは、「これくらいの値になるだろう」と、平均を予想するものです。
パチンコで期待値を求めるときのざっくりイメージは、こんな感じ。
平均出玉=(確変突入率×確変のときの出玉)+(非突入率×確変にならないときの出玉)
期待値の求め方は、えらく長くなるので(汗)。
高校生向きに「期待値とは?計算方法と具体例をわかりやすく解説【高校1年生向け】」という記事で書いています。
実際の計算例は、大工の源さんを例に
平均出玉=Rush突入+Rush非突入=3,720.36玉+238.8玉=3,959.16玉
みたいに、「継続率93%の平均継続数は14.3連。求め方についても解説」で説明しているので、そちらを見てください。
ボーダー理論は嘘なのか?そのまま実践しても勝てない

それじゃあ、結局ボーダー理論って嘘なの?本当なの?
と言われると、なかなか難しい問題です汗。
ボーダー理論が当てはまる人もウソの人もいる
ふんわりとした言い方になって申し訳ないのですが、「ボーダー理論が当てはまる人もウソの人もいる」が答えです。

え?言ってる意味が全然分からん・・・。
と思った人が大半ですよね。
ボーダー理論は確率通り出玉が出る前提のもの
ボーダー理論は、そもそも論的に「確率通りになる前提(期待値通りに玉が出る前提)」で考えられています。

確率通りになる前提・・・

裏を返せば、確率通りに出なければボーダー理論は、そのまま使えないってことです!
打てる時間が限られている以上は、誤差を考えないとダメ
パチンコって、サラリーマンや自営業やっている方なら、打てる時間は限られています。
メーカーやパチンコ屋さんがイカサマやっているかは、別にして(汗)。
最近は、海物語や花の慶次、北斗(と言っても無双だけ)くらいでないと、すぐに撤去されます。

初当たり数回だけ当たって、もう一回打とうとしたけど。
いつのまにか撤去なんてこともありますよね・・・。
となると・・・。
北斗無双(この記事書いたとき、今ならエヴァ15)くらい打ち込んでも、確率通りになる保証はないが、それでもボーダー理論はあてになるのか?
ということを考えないといけません(つまりは、誤差があるよねって話)。
ボーダー理論以外に考えるべき確率の壁は信頼区間
ひよこSEは、ボーダーラインに加えて、確率の壁がもう一つあると思っていて。
「信頼区間」というものがあるので、信頼区間込みのボーダーを考えてあげないと、パチンコでは勝てません。

なんじゃそりゃ!

ざっくりといえば、「95%の確率で、これくらいの数字になるよね~」というものです。
まぁ、「信頼区間」の正体が、いわゆる「相性」とか「誤差」という話になるのですが・・・(統計学的には、「分散」)。
信頼区間は、「95%の確率で、これくらいの数字になるよね」というもの
信頼区間について説明すると、「95%の確率で、これくらいの数字になるよね」というものです。
例えば、ほとんどの人が、イヤ~な思いをしているであろう北斗無双の平均出玉は、4,600玉程度。
300玉くらいの誤差は許容するとして。
「北斗無双で初当たり100回取ったときの平均出玉の95%信頼区間は、4,300~4,900玉の間」
みたいに使ったりします。

う~ん。よくわからない。
つまりはこういうことです。
- 初当たり100回取った人の95%は、平均出玉が4,300~4,900玉になる。
- 初当たり100回取った人の2.5%は、平均出玉が4,299玉以下になる。
- 初当たり100回取った人の2.5%は、平均出玉が4,901玉以上になる
※誤差が何玉になるのかは、実際にはキチンと検証しないとダメだけど、大学レベルの話でだるいので許してください 笑
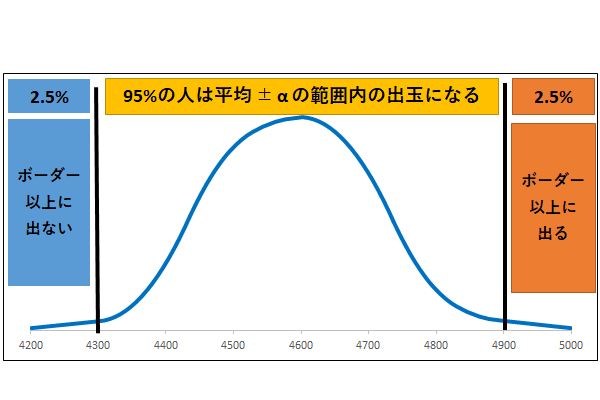
信頼区間を言い換えると「相性」とか「誤差」になる

え?2.5%の人は、4,299玉以下って・・・悲惨じゃん。

これが、よく言われる「この台とはなぜか、相性がいい(悪い)」みたいな話です。
95%の人は、特定の範囲内(つまりは、期待出玉の誤差の範囲内)におさまります。
その一方で、2.5%の人は「全然この台、出ないじゃん」みたいに出玉が少なくなります。
さらにその一方で、2.5%の人は「この台、めっちゃ出る!お宝台」みたいに出玉が多くなります。
信頼区間を仮定して、ボーダーをもう一度出してみる
さて、95%信頼区間が4,300~4,900だと仮定したとき。
北斗無双の等価ボーダーを出し直すとこんな感じ。
95%の人は、16.311~18.587が北斗無双の実践上のボーダーラインになります。
それでも、
- 2.5%の人は、16.311より回らない台でも、なぜか勝てる
- 2.5%の人は、18.586より回る台を打っても負けてしまう
不思議な感じがするのが、パチンコというか、確率・統計学の世界なのです(´▽`*)。
まとめ:「ボーダー以上かつ相性が良い」をクリアしないと勝てない
話がかなり難しくなりましたが、この記事で言いたかったことは・・・。
「ボーダー以上かつ相性が良い」をクリアしないと勝てないということです。
その説明として、「95%の人は、ボーダーはこの辺になる」というのを計算できる「信頼区間」というものがあって。
最低でも、95%信頼区間内で、いちばん低い出玉の分のボーダーがないと厳しい。
それでも、2.5%の人は、ボーダー+1~2くらいでは、誤差の範囲で負けてしまう世界。
真剣に考えれば考えるほど、パチンコで安定して勝つのは難しいという話でした(-_-;)。

コメント