期待値とは？計算方法と具体例をわかりやすく解説【高校１年生向け】

どうも！ひよこSE（@PiyoOct）です。

期待値を数Aで勉強したけど、わけわかんない。

「これくらいの値になるだろう」という予想するのが期待値！

さて、「これくらいの値になるだろう」と予想するのが期待値ですが、押さえておくべきポイントは、たった一つ。計算方法だけです。

期待値の計算方法

「確率×なんかの値（サイコロの目・点数とか金額）を全部の事象で求めて足す」

これが理解できていれば、期待値は楽勝です！

期待値とは、平均の予想のようなもの
期待値の計算方法
期待値の具体例は？
期待値の演習問題（文章題）２問
期待値の文章題の回答

期待値とは、平均の予想のようなもの

そもそも、期待値って何？何のために出すの？

「これくらいの値になるだろう」と平均を予想するのが期待値！

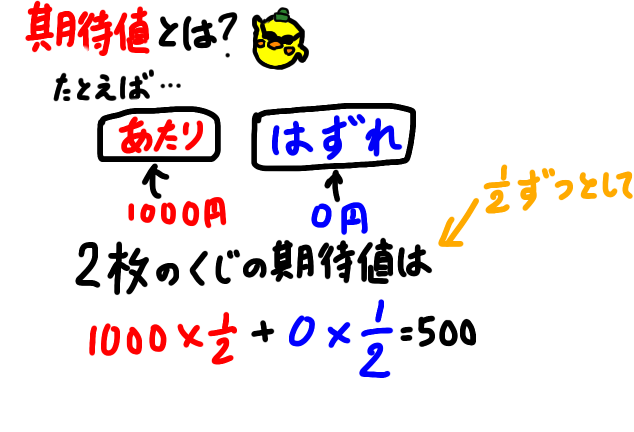
平均を予想するために、確率となんかの値をかける

「平均を予想する」ために、期待値というのがあります。

あくまでも予想です。

ってことは、あてにならなかったりする？

・・・その通りです。

実際にどうなるかは、また別問題です。

あくまでも、「●●のようになることが期待できる」っていうのを求めます。

平均と期待値の違い。平均は実際の値で、期待値は予想

平均と期待値って、似ているよね？何が違うの？

期待値は、あくまでも予想。平均は実際の値です！

例えば、テストの平均点をイメージしてください。

平均点を求める方法は、学年なり、クラス内の生徒が取った点数の合計を人数でわってあげれば、求めることができますよね！

（平均点）＝（全生徒の合計点）÷（人数）

あるテストで、Aくん50点・Bくん60点・Cちゃん100点なら平均点は、

(50点+60点+100点)÷(3人)=210÷3=70

70点が平均点です。

反対に、期待値は、「予想」です。

予想なので、理論上の値です。

例えば、Aくん50点・Bくん60点・Cちゃん100点を取ったテスト。

難易度が同じようなテストをもう一度すれば、「たぶん平均点は70点」になりますよね。

期待値は、この、「たぶん」を確率を使って求めに行きます。

ここら辺の理屈は、テストには出ないので、これから説明する計算方法だけ知っておけば問題なしです！

期待値の計算方法

期待値の計算方法は、「確率×なんかの値（サイコロの目・点数とか金額）を全部の事象で求めて足すこと」です。

例）1/2の確率で1000円の当たりが出るが、1/2でハズレ、0円となるくじがあったとします。

このくじの期待値を計算してあげると、500円となります。

「確率×なんかの値（サイコロの目・点数とか金額）を全部の事象で求めて足す」

＝(当たりが出る確率×1000円)＋(ハズレが出る確率×0円)

＝(1/2×1000)+(1/2×0)

=500+0=500

期待値の具体例は？

期待値の身近な具体例は、パチンコとか宝くじ、サイコロの目あたりですね。。。

例えば、サイコロの目は1,2,3,4,5,6の6つ。それぞれの出現確率は、すべて同じ。1/6です。

なので、サイコロの目の数字を期待値にすると、

(1の目が出る確率×1)＋(2の目が出る確率×2)＋(3の目が出る確率×3)＋(4の目が出る確率×4)＋(5の目が出る確率×5)＋(6の目が出る確率×6)

=(1/6×1)+(1/6×2)+(1/6×3)+(1/6×4)+(1/6×5)+(1/6×6)

=(1+2+3+4+5+6)/6

=21/6=7/2~~（3.3333333・・・）~~（3.5）⇒指摘いただいた方、大変失礼しました(-_-;)。

サイコロの目の数字を平均すると、~~3.3くらい~~3.5になるってことですね！

期待値の暗黙の了解として、整数にならない場合で、問題文に何も書かれてない場合は、約分したうえで分数のままで問題なしです！

期待値の演習問題（文章題）２問

期待値の演習問題（文章題）２問を作ってみたので、チャレンジしてください！

大問１

とあるじゃんけん大会で、参加費の1,000円を支払って、主催者とじゃんけんを行う。

参加者が勝ちの場合は、1,500円
あいこの場合は、800円
主催者が勝ちの場合は、400円

上記のように賞金がもらえる場合、次の(1)～(3)の問に答えよ。

(1)このじゃんけん大会で、参加者が得られる賞金の期待値を求めよ

(2)このじゃんけん大会に参加するのは、損であるか得であるかを答えよ

(3)参加費1,000円を上回る期待値となるのは、参加者が勝ちの場合の賞金がいくら以上の場合か？

※ただし、あいこの場合の賞金と、主催者が勝ちの場合の賞金は、変わらないものとする。

大問２

1～6の目が刻まれた、大きさが異なるサイコロが2個ある。

大小2個のサイコロを振ったときに出た数字の積に応じて、下記のように得点をつける。

出た目の積が偶数の場合は、積を1/2して、得点とする。
出た目の積が奇数の場合は、積を2倍して、得点とする。
ただし、ゾロ目（2個とも同じ目）の場合は、積ではなく、和を得点とする。

この場合、大小2個のサイコロを振ったときの得点の期待値を求めなさい。

期待値の文章題の回答

期待値の文章題の回答を書きますね！

大問１：いさぎよく書き出す

まとめると、

参加費は1000円
参加者が勝ちなら1500円
あいこなら800円
主催者が勝ちの場合は、400円

ですね。

じゃんけんは、知っている人は知ってると思いますが、勝ち・あいこ・負けの確率はすべて同じで、1/3です。

知らなかったとしても、いさぎよく書き出せばOK！

参加者の手	主催者の手	参加者の勝ち・あいこ・負け
グー	グー	あいこ
グー	チョキ	勝ち
グー	パー	負け
チョキ	グー	あいこ
チョキ	チョキ	勝ち
チョキ	パー	負け
パー	グー	あいこ
パー	チョキ	勝ち
パー	パー	負け

(1)このじゃんけん大会の期待値は、

(1/3×1500)+(1/3×800)+(1/3×400)

=(1500+800+400)/3=2700/3=900

900円（答え）

(2)じゃんけん大会の参加費は、1000円であるのに対して、(1)より期待値は900円。

したがって、参加するのは損である。（答え）

参加するたびに、100円なくなっていく計算・・・

(3)参加者が勝ちの場合の賞金をXとする。

参加費1000円を上回るためには、

(1/3×X)+(1/3×800)+(1/3×400)>1000

(X+800+400)/3>1000

(X+800+400)>3000

X>1800

つまり、賞金の期待値が、参加費を上回る場合は、

参加者が勝ちの場合の賞金が1801円以上（1800円より大きい）となる。（答え）

勝ちの場合の賞金をXとするのは、できてほしい！

大問２：いさぎよく書き出す

大きさが異なるサイコロ
出た目の積が偶数の場合は、積を1/2して、得点とする。
出た目の積が奇数の場合は、積を2倍して、得点とする。
ただし、ゾロ目（2個とも同じ目）の場合は、積ではなく、和を得点とする。

このルールで、サイコロの目と得点を書き出すと下記の通りとなる。

（小）の目／（大）の目	1	2	3	4	5	6	よこの得点計
1	2	1	6	2	10	3	24
2	1	4	3	4	5	6	23
3	6	3	6	6	30	9	60
4	2	4	6	8	10	12	42
5	10	5	30	10	10	15	80
6	3	6	9	12	15	12	57
たての得点計	24	23	60	42	80	57	286