どうも!ひよこSE(@PiyoOct)です。

階乗、わけわかんない
となってしまった、高校1年生向けに解説します(基礎の基礎なので、受験生向けではないです)。
教科書を見ると、
N!=N!=N(N-1)(N-2)・・・1
みたいな文字の計算式がいきなり出てくるので、「ゲゲッ(´▽`*)」となったかもしれません。
見た目は難しそうに思えても、大丈夫。実は、すごくシンプルな話です。
「階乗とはなにか?」についてですが、「ビックリマークの頭の数字から1になるまで掛ける」と覚えてしまいましょう。
これから、計算方法・計算例について解説するとともに、最後に問題を用意したので解いてみてくださいね!
階乗とは?頭の数字から1になるまでかけて計算すればよし
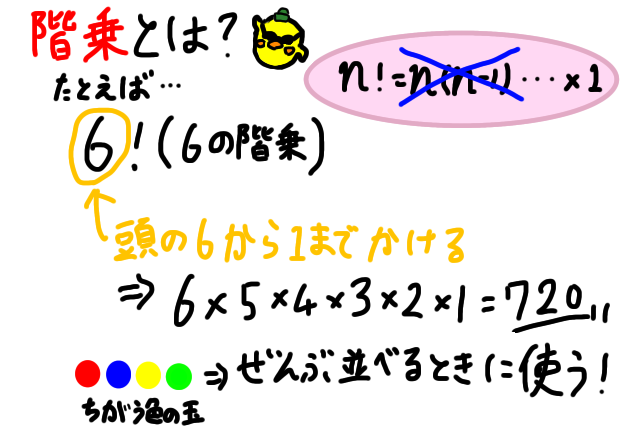
階乗は、ビックリマークの頭の数字から1になるまでかけて計算すればよしです。
なので、6!(6の階乗)であれば、「6から1になるまでかける」ので、
6!=6×5×4×3×2×1=720
たった、これだけです。
階乗の公式を教科書やWikipediaっぽく言うと、「自然数1からNまでの積」なので
N!=N!=N(N-1)(N-2)・・・1
となります。

なんだか、難しそう・・・
・・・が、公式の通りに難しく考える必要は一切ありません。。。
階乗の計算例
階乗の計算例を挙げます。
例えば、
- 7!(7の階乗)であれば、「7から最後の1までかける」
- 6!(6の階乗)であれば、「6から最後の1までかける」
- ・・・(中略)
- 1!(1の階乗)であれば、「1から最後の1までかける」
と考えてあげればいいので、
- 7!=7×6×5×4×3×2×1=5040
- 6!=6×5×4×3×2×1=720
- 5!=5×4×3×2×1=120
- 4!=4×3×2×1=24
- 3!=3×2×1=6
- 2!=2×1=2
- 1!=1=1
- 0!=1
となります。

7の階乗(7!)あたりまでは、よく出てくるので、答えを丸暗記するのもあり!
0の階乗(0!)は、どうして1なの?

ところで、どうして0の階乗(0!)は0じゃなくて1なの?
例えば、7!÷0!を計算するとします。
もし、「0!=0」としてしまうと、7!=5040なので、
7!÷0!=5040÷0=∞(無限大)

数字を0で割ると、答えは無限大です。スマホの電卓で試すと、エラーになるはず。
「無限大」が答えなのは、困っちゃいますよね。なので、仕方なしに「0!=1」とします。
それか、「0!ということは、なにもないとカウントして1」と覚えてもらってもOKです。
・・・数学的な証明として、なぜ0!=0でないかは、ひよこSEには証明はできません(´▽`*)。
階乗とは何につかうのか?

階乗ってどんなときに使うの?
っていうのが、わかってないと「6!=720」みたいに丸暗記しても、実際は文章題として出題されるので、意味ないですよね。
キーワードは、並び替える際に
- 「区別できる場合」で、「そこにあるものすべてを並び替える場合」
の2つが、当てはまる場合。
「区別できる場合」で、「そこにあるものすべてを並び替える場合」は、階乗で計算をします。

これから例を挙げます。
正直、感覚の部分もあるので、演習しつつ覚えていってください。
■区別できる場合の例
- 赤・青・緑・黄色の異なる色の玉4つ
- 人が並ぶ場合(区別できるって言い方は適切ではないですが、便宜上、勘弁してください)
■区別できないの場合の例
- 同じ色の白玉5つ
■「そこにあるものすべてを並び替える場合」の例
- 赤・青・緑・黄色の異なる色の玉4つすべてを並び替える
- Aくん、Bさん、Cくん、Dさんの4人全員が整列する
■「そこにあるものすべてを並び替える場合」があてはまらない例
- 赤・青・緑・黄色の4つの異なる色の玉の中から2つを選んで並び替える(階乗ではなく、順列)
- Aくん、Bさん、Cくん、Dさんのうち、2人だけが呼ばれる場合(階乗ではなく、順列)
階乗の計算問題・文章題を7問演習
それでは、階乗の計算問題5問、文章題2問の計7問を演習して、知識を固めましょう。

答えは、一番最後に書いておくので、見てくださいね。
階乗の計算問題5問
(1)~(5)の値がいくつになるか答えなさい。
(1)7!
(2)(5+3)!
(3)(4-4)!
(4)2!+4!
(5)3!×6!
階乗の文章題2問
(6)Aくんは、白・黒・赤・青・黄の異なる色のついた玉を5つ持っている。
この5つの玉を横に並べるときに、並べ方は全部で何通りあるか?
(7)太郎くん、花子ちゃん、一郎くん、二葉ちゃんの4人がいる。
先生が、4人に対して一列に整列するように呼び掛けたとき、4人の並び順は全部で何通りあるか。
階乗の計算問題・文章題の答え
(1)7!=7×6×5×4×3×2×1=5040
(答え)5040

7から最後の1まで順番にかける!
(2)(5+3)!=8!=8×7×6×5×4×3×2×1=40320
(答え)40320

階乗の時も、かっこの中を先に計算するルールは変わらない!
(3)(4-4)!=0!=1
(答え)1

0の階乗をうっかり、0と答えないように!
(4)2!+4!=(2×1)+(4×3×2×1)=2+24=26
(答え)26
(5)3!×6!=(3×2×1)×(6×5×4×3×2×1)=6×720=4320
(答え)4320

階乗同士の四則演算(足す・引く・かける・わる)は、階乗を先に計算した後にすればよし!
(6)白・黒・赤・青・黄の異なる色のついた玉を5つを並べる方法は全部で、
5!=5×4×3×2×1=120
なので、120通りである。
(7)太郎くん、花子ちゃん、一郎くん、二葉ちゃんの4人が一列に並ぶ方法は全部で、
4!=4×3×2×1=24
なので、24通りである。

すべてのものや人を並べる場合は、階乗と覚えておこう!
階乗については、以上になります。ここまで読んでくれてありがとうございました。

コメント