どうも!ひよこSE(@PiyoOct)です。

順列、わけわかんない。階乗や組合せともごっちゃになった・・・
となってしまった、高校1年生向けに解説します(基礎の基礎なので、受験生向けではないです)。
階乗⇒順列⇒円順列⇒組合せの順で学習した記憶(間違ってたらすみません(´▽`*))がありますが、もう2つ目の順列でお手上げ状態の人もいるかと思います。
なお、階乗について自信がない人は「階乗とは?計算方法・計算例をわかりやすく解説【高校1年生向け】」も読んでくださいね!
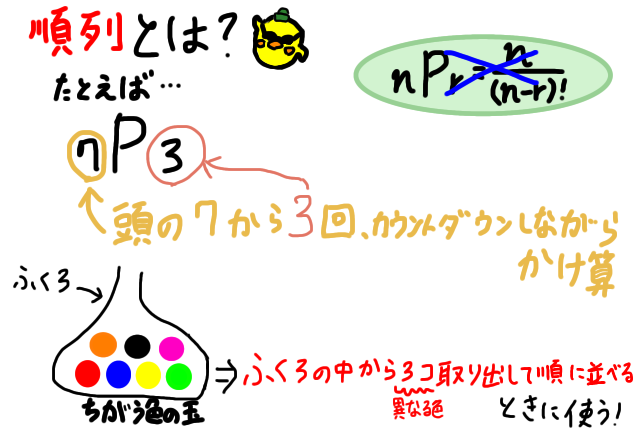
さて、「順列とはなにか?」ですが、「Pの前の数字から、Pのうしろの回数だけカウントダウンしながらかけ算する」と覚えてしまいましょう。
「8P2」なら、「Pの前の8から2回カウントダウンしながらかけ算する」ので、「8×7=56」が答え。
これから、順列について、計算方法と使い方について解説するとともに、最後に問題を用意したので解いてみてくださいね!
順列とは?計算方法について解説
順列でよく見る公式たち・・・。
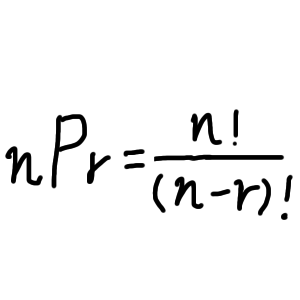
こういうのを考えると難しいので、いっそのこと、公式は覚えるのやめましょう。この式がテストに出ることはないです。
なので、「順列とはなにか?」となれば、「Pの前の数字から、Pのうしろの回数だけカウントダウンしながらかけ算する」と、条件反射的に覚えましょう。
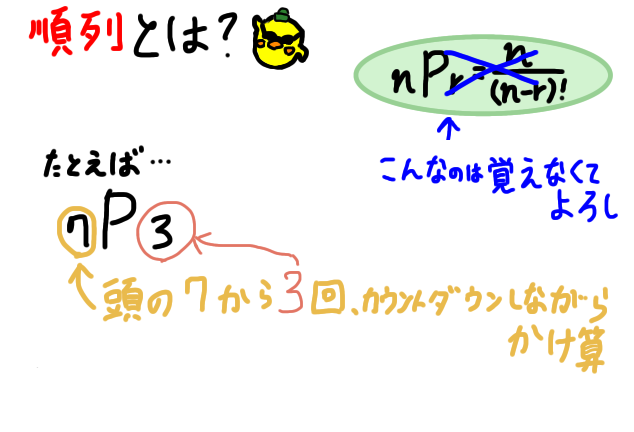
7P3=「Pの前の7から、3回だけカウントダウンしながらかけ算」
=7×6×5=210
たった、これだけです。
順列の計算例
順列の計算例を挙げます。

こういうのは、見ながら・書きながら覚えていくのが一番!
例えば、
- 5P3であれば、「Pの前の5から、3回だけカウントダウンしながらかけ算」
- 6P4であれば、「Pの前の6から、4回だけカウントダウンしながらかけ算」
- 7P5であれば、「Pの前の7から、5回だけカウントダウンしながらかけ算」
- 8P1であれば、「Pの前の7から、1回だけカウントダウンしながらかけ算」
と考えてあげればいいので、
- 5P3=5×4×3=60
- 6P4=6×5×4×3=360
- 7P5=7×6×5×4×3=2520
- 8P1=8
となります。
順列を使う場面はどんなとき?
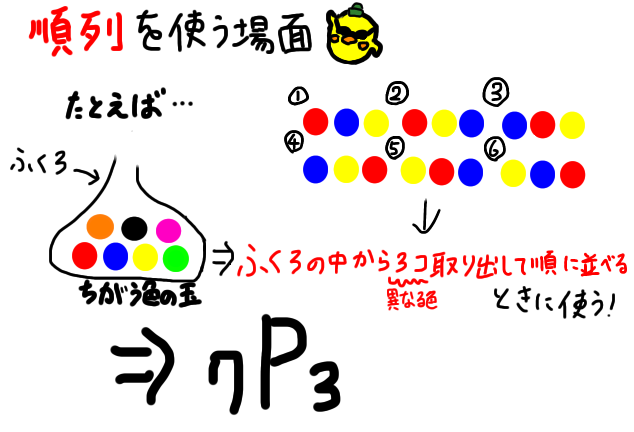

順列を使う場面ってんなとき?
っていうのが、わかってないと「4P2=12」みたいに計算できるだけでは、実際は文章題として出題されるので、お話になりません。
キーワードは、並び替える際に
- 「区別できる場合」で、「その中から全部でなく、いくつか選んで並べる場合」
- 「区別できる場合」で、「その中から全部でなく、1つずつ順番に選ぶ場合」
の2つが、当てはまる場合。
「区別できる場合」で、「その中から全部でなく、いくつか選んで並べる場合」は、順列で計算をします。

階乗についての記事の例とかぶりますが、おさらいをかねて、ここでも例を挙げます。
正直、感覚の部分もあるので、演習しつつ覚えていってください。
■区別できる場合の例
- トランプのスート(ハート・ダイヤ・クローバー・スペード)

余談ですが、スート(英語でsuit)と言えるとなんだか、かっこいい!
■区別できないの場合の例
- 同じ色の白玉5つ
■「その中から全部でなく、いくつか選んで並べる場合」の例
- 赤・青・緑・黄色の4つの異なる色の玉の中から2つを選んで並び替える
- Aくん、Bさん、Cくん、Dさんのうち、2人だけが順番に呼ばれる場合
■選ぶだけの例
- 袋の中の異なる色の玉6つを同時に3つ取り出す場合
順列と組合せの区別にどうしても苦労する場合は、
で、多少はイメージできるはず。。。
順列の計算問題・文章題を7問演習
それでは、順列の計算問題3問、文章題4問の計7問を演習して、知識を固めましょう。

答えは、一番最後に書いておくので、見てくださいね。
順列の計算問題3問
(1)~(3)の値がいくつになるか答えなさい。
(1)10P4
(2)13P2
(3)9P6
順列の文章題3問
(4)Aくんは、白・黒・赤・青・黄・緑の異なる色のついた玉を6つ、袋に入れた。
この6つの袋の中の玉の中から3つを選んで順番に並べる場合、並べ方は全部で何通りあるか?
(5)太郎くん、たけしくん、一郎くん、花子ちゃん、二葉ちゃん、かおりちゃんの6人(男子3人・女子3人)がいるとき、先生が横に整列するように呼び掛けた。次の(ア)~(ウ)について答えなさい。
(ア)太郎くんと花子ちゃんが、必ず隣になる並び方は何通りあるか?
(イ)男子と女子が交互になる並び方は、何通りあるか?
(ウ)男子3人同士・女子3人同士がそれぞれ隣になる並び方は、何通りあるか?
階乗の計算問題・文章題の答え
(1)10P4=10×9×8×7=5040
(2)13P2=13×12=192
(3)9P6=9×8×7×6×5×4=9×8×7×6×20=60480

偶数×5を先に計算すると、一の位が必ずゼロになるから計算が楽!
(4)袋の中にある、白・黒・赤・青・黄・緑の異なる色のついた玉を6つの中から3つを選んで並べる方法は、
6P3=6×5×4=120なので、120通りである。(答え)
となり合うときたら、Xに置き換える
(5)(ア)太郎くんと、花子ちゃんはカップルなのでしょうね(´▽`*)。
並び方の例を挙げると・・・
- 太郎・花子・たけし・一郎・二葉・かおり
- 花子・太郎・たけし・一郎・二葉・かおり
太郎と花子の二人は、いろんな意味(?)で離れることはありません。
なので、2人一組、さらに言えば、あたかも1人のように一心同体(意味深)に「X」として扱ってあげます。
すると、
- X・たけし・一郎・二葉・かおり
の5人全員を並び替える方法は、5!=120。
そして、Xというのは、太郎・花子の2人。太郎と花子は、左右どちらに並んでもいいので、二人の並び方は、2!=2。
つまり、5人全員を並び替えながら、太郎と花子の2人の並び順を考慮すると、並び方は下記の通り。
5!×2!=120×2=240通り(答え)
「2つ以上のものがとなり合う」問題では、必ずXとして一つにする。
・・・ちなみに、

階乗の問題じゃないか!
と思った人もいるかもしれませんが、「となり合うパターン」は、順列の時に覚えたほうが楽なのです(-_-)。
交互の時は、先にどちらかを並べる。そのすき間に残ったほうを並べる
交互に並ぶパターンも頻出。
こういう時は、男子と女子をグループ化。どちらか片方を先に並べてあげます。
交互ときたら、同じグループのもの・人のうちの片方を先に並べる!
男子を先に並び替える場合、女子を先に並び替える場合のどちらも、3!=6通り。
今回は男子を並び替えたとして、話をすすめると
「男子男子男子」となっている状態。
そこから、女子が間に入るイメージ。この「間に入る」っていうのが重要です。
つまり・・・
〇男子●男子●男子〇
●の部分に、女子2人。
〇の部分に、女子1人が入れば、男子と女子は、必ずとなり合います。

○4つとしたいところだけど、女子男子男子女子男子女子のパターンがあるから、この場合はNG!
- ●の部分に女子2人が入るのは、3人のうち2人が2つの●に入るということなので、3P2=6
- ○の部分に女子1人が入るのは、1人が2つの○に入るということなので、2P1=1
したがって、男子と女子が交互に並ぶ方法は、男子の並び方×◎の並び方×○の並び方となるので、
3!×3P2×2P1=6×3×2=36通り(答え)となります。
グループを作るときも、X・Yなど使う
きっと男子と女子がケンカしたのでしょう(´▽`*)。
男子男子男子・女子女子女子と並ぶ問題です。

感覚をつかむと、(5)(ア)の発展と気づくはず!
(5)(ア)男子をX、女子をYとします。
男子男子男子/女子女子女子となるので、X/Yとなりましたね。
XとYを並び替える方法は、2!=2×1=2通り
X同士、つまり男子3人同士はどの順番で並んでもよし。
男子3人同士を並び替える方法は、3!=6通り。
Y同士、つまり女子3人同士も同様に、3!=6通り。
なので、XとYを並び替えて、男子3人と女子3人も並び替えられるので、
2!×3!×3!=2×6×6=72通り(答え)
となります。
順列については、以上になります。ここまで読んでくれてありがとうございました。

コメント