組合せとは？計算方法と使う場面をわかりやすく解説！【高校１年生向け】

どうも！ひよこSE（@PiyoOct）です。

となってしまった、高校１年生向けに解説します（基礎の基礎なので、受験生向けではないです）。

「階乗と順列までは、何とか理解できた！」という人も、組合せが出てきた瞬間にごっちゃになるなんてこともしばしば。

ひよこSEが高校生だった時、組合せが一番苦労しましたね。

さて、「組合せとはなにか？」ですが、「Cの前の数字から、Cのうしろの回数だけカウントダウンしながらかけ算。Cの後ろの数字の階乗でわる」と覚えてしまいましょう。

「8C3」なら、「Cの前の8から3回カウントダウンしながらかけ算。Cのうしろの数字の階乗でわる」ので、「（8×7×6）÷（3×2×1）=56」が答え。

Cのうしろの階乗でわるときは、

(8×7×6)÷(3×2×1)＝56

「6」と「3×2」のように、割り算の前後（割る側と割られる側）で同じ値になるものを消してやると計算がラクです！

これから、組合せについて、計算方法と使い方について解説するとともに、最後に問題を用意したので解いてみてくださいね！

組合せとは？計算方法について解説

組合せでよく見る公式たち・・・。

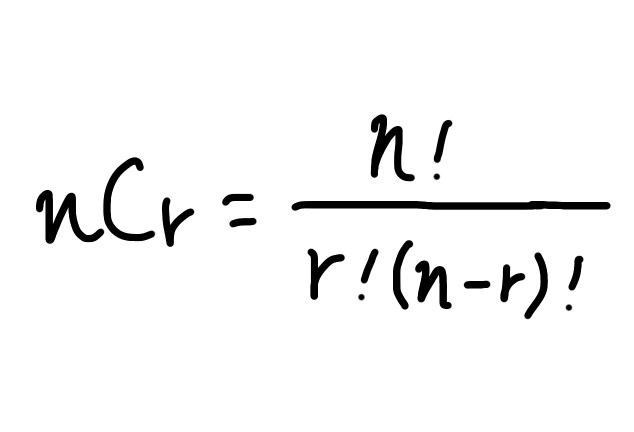
こういうのを考えると難しいので、階乗や順列と同様に、公式は覚えるのやめましょう。

この式がテストに出ることはないです。

なので、「組合せとはなにか？」となれば、「Cの前の数字から、Cのうしろの回数だけカウントダウンしながらかけ算。Cの後ろの数字の階乗でわる」と、条件反射的に覚えましょう。

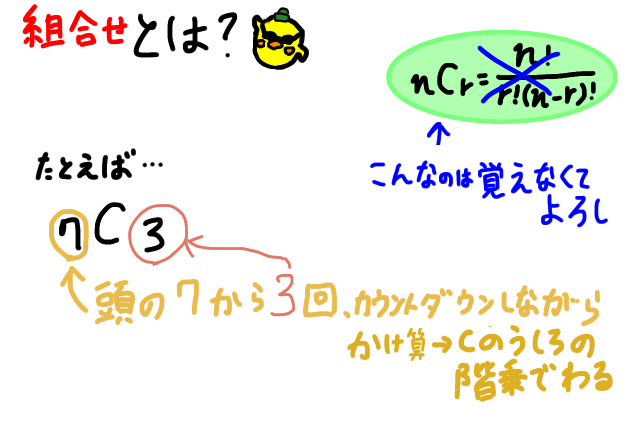
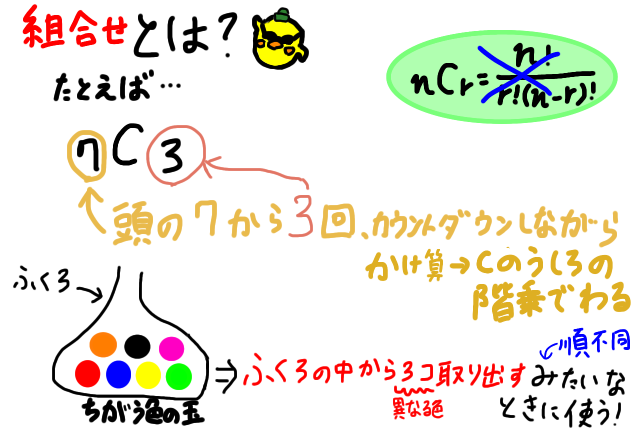
7C3=「Pの前の7から、3回だけカウントダウンしながらかけ算。Cの後ろの3の階乗でわる」
=7×6×5÷(3×2×1)=7×6×5÷(3×2×1)=35

たった、これだけです。

組合せの計算例

組合せの計算例を挙げます。

例えば、

と考えてあげればいいので、

となります。

組合せを使う場面はどんなとき？

っていうのが、わかってないと「8C3＝56」みたいに計算できるだけでは、ダメ。

組合せまで習うと、いくらでもひねった文章題が出題できるので、公式の丸暗記は通用しません。

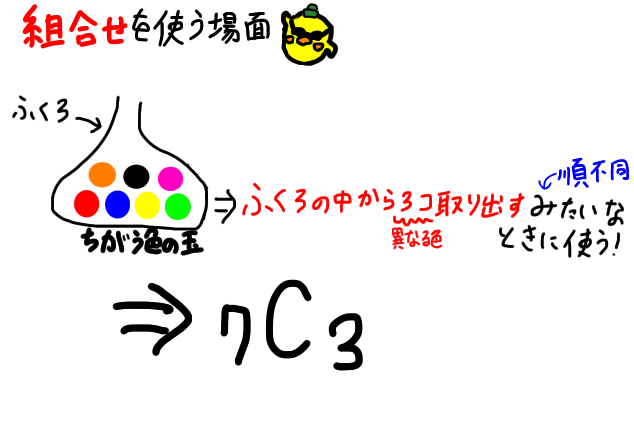
キーワードは、並び替える際に

• 「色や番号のように区別できる場合」で、「その中から全部でなく、いくつか選ぶだけの場合」

が、当てはまるとき。

■区別できる場合の例

• 袋の中の玉の色がすべて異なる場合

■区別できない場合の例

• 袋の中の玉の色がすべて同じ場合

■選ぶだけの場合の例

• 袋の中の異なる色の玉６つを同時に３つ取り出す場合

■選んで並べる場合の例

• トランプのスート（ハート・ダイヤ・クローバー・スペード）を、順番に並べる

組合せの計算問題・文章題を７問演習

それでは、組合せの計算問題３問、文章題４問の計７問を演習して、知識を固めましょう。

組合せの計算問題３問

（１）～（３）の値がいくつになるか答えなさい。

（１）10C3

（２）13C4

（３）11C2

組合せの文章題３問

（４）Aくんは、白・黒・赤・青・黄・緑の異なる色のついた玉を６つ、袋に入れた。

この６つの袋の中の玉の中から３つを選ぶとき、選び方は全部で何通りあるか？

（５）1～9までの数字が書かれたカードがあるとき、次の（ア）～（ウ）について答えなさい。

（ア）カード３枚を選ぶときの選び方の総数と、３枚とも偶数になる選び方はそれぞれ何通りか？

（イ）カード３枚を選んで並べるとき、偶数になる選び方は何通りか？

（ウ）カード３枚を選ぶとき、少なくとも１枚は偶数になる選び方は何通りか？

組合せの計算問題・文章題の答え

（１）10C3＝(10×9 3 ×8 4 )÷(3×2×1)=10×3×4=120

（２）13C4＝(13×12×11×10 5 )÷(4×3×2×1)=13×11×5=143×5=715

（３）11C2＝(11×10 5)÷(2×1)=11×5=55

（４）袋の中にある、白・黒・赤・青・黄・緑の異なる色のついた玉を６つの中から３つを選ぶ方法は、

6C3＝(6×5×4)÷(3×2×1)=5×4=20なので、２０通りである。（答え）

選んだものすべてが○○ときたら、条件に当てはまる数を確認！

（５）（ア）１～９のカードのうち、３枚を選ぶ選び方の総数は、

9C3=(9 3×8 4 ×7)÷(3×2×1)=84（通り）（答え）

また、偶数のカードは2,4,6,8の4枚であり、3枚すべて偶数になる選び方は、偶数のカード4枚の中から3枚を選ぶ選び方と同じである。

したがって、4C3=(4×3×2)÷(3×2×1)=4（通り）（答え）

どこか一か所に条件があるときは、先にピックアップして残りを並べる

（５）（イ）１～９のカードのうち３枚を選んで並べるときに、偶数となる条件は、一の位が2,4,6,8となる並べ方である。

この条件を満たす並べ方は、

となるので、一の位×十の位・百の位=4C1×8P2=4×8×7=224（通り）（答え）

少なくとも○○ときたら即、反対の場合を考えて引き算

少なくとも○○ときたら即、反対の場合を考えて引き算します。

今回の場合は、

「カード３枚を選ぶとき、少なくとも１枚は偶数になる選び方」

の反対は、

「カード３枚を選ぶとき、すべて奇数になる選び方」

になります。

カード３枚を選ぶ総数は、（ア）より、84通り。

カード３枚を選ぶとき、すべて奇数になる選び方は、奇数のカードは1,3,5,7,9の5枚。

この5枚の中から3枚を選ぶのと同じなので、

5C3=(5×4×3)÷(3×2×1)=10通り

である。

これは、「カード３枚を選ぶとき、少なくとも１枚は偶数になる選び方」の反対の選び方なので、

（少なくとも１枚は偶数になる選び方）＝(総数)-(すべて奇数の選び方)＝84-10=74（通り）（答え）

組合せについては、以上になります。ここまで読んでくれてありがとうございました。