バブルソート(基本交換法)とは、先頭から順に、となり合うデータを比較して並び替えるプログラムのつくり、アルゴリズムのことです。
バブルソートは、基本交換法って呼ばれたりもしますが、「バブルソート」のほうが個人的には、なじみがあります。
図解にして、わかりやすく書くとこんな感じ。
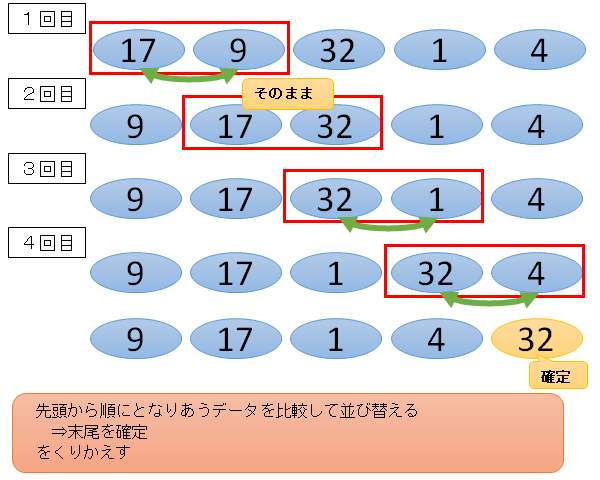
- 先頭から順番に、となり合うデータを比較して並び替える
- 末尾を確定
- 1・2を末尾の1個前から、先頭までくりかえす
先頭から順番にデータを並び替えているので、末尾の1個前(上の図だと4回目の”32”)と末尾(上の図だと4回目の”4”)は、どちらかが最大値、つまりは末尾の数字というわけです。
バブルソートのやりかた
バブルソートのやりかたは、冒頭に書いた通りですが、再掲します。
- 先頭から順番に、となり合うデータを比較して並び替える
- 末尾を確定
- 1・2を末尾の1個前から、先頭までくりかえす
[17, 9, 32, 1, 4]
の5つの数字のバブルソートを、1~3の手順で最後まで行います。

※余談だけど、「バブルソート」=”bubble sort”=「泡のように並び替える」なので、青色の円にしています(*´ω`)。
末尾(5番目の数字)の確定
まず、末尾の数字を確定させるために、先頭から順番に、末尾まで並び替えを行います。
■先頭と2番目の数字
17と9だと、17の方が大きいので、右に並び替えます。
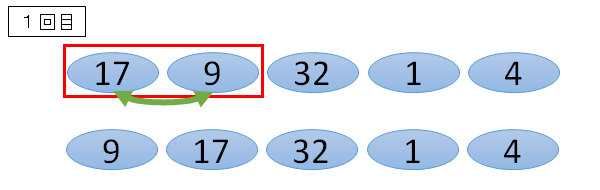
■2番目と3番目の数字
17と32だと、17の方が大きいので、そのまま。並び替えは行いません。

■3番目と4番目の数字
32と1は、32の方が大きいので、並び替えます。
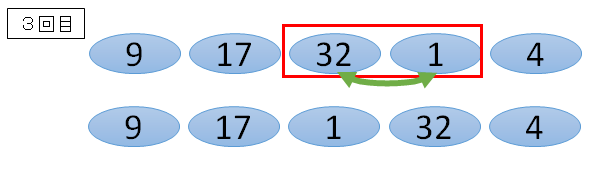
■4番目と5番目の数字
32と4は、32の方が大きいので、並び替えます。
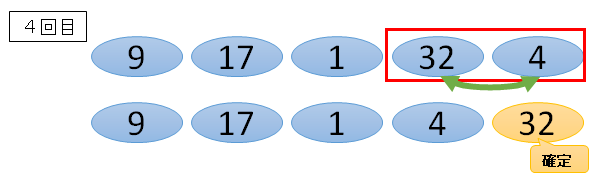
■末尾(5番目)の数字が確定
バブルソートでは、先頭から順番にデータを並び替えています。
なので、末尾の1個前(上の図だと4回目の”32”)の数字は、末尾以外の数字の中の最大値。
最後に、末尾(上の図だと4回目の”4”)と比較してあげれば、どちらかが末尾の数字として確定します。
今回だと、32と4を並び替えたので、「32が末尾の数字」として確定します。
4番目の数字の確定
次に、4番目の数字を確定させるために、先頭から順番に、4番目まで並び替えを行います。
■先頭と2番目の数字
9と17だと、17の方が大きいので、そのまま。並び替えは行いません。

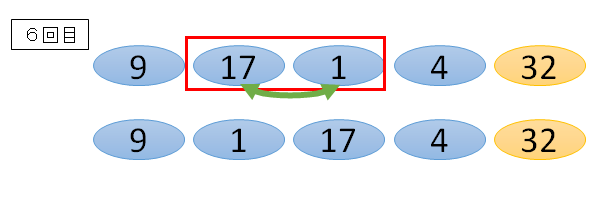
■2番目と3番目の数字
17と1だと、17の方が大きいので、右に並び替えます。
■3番目と4番目の数字
17と4だと、17の方が大きいので、右に並び替えます。
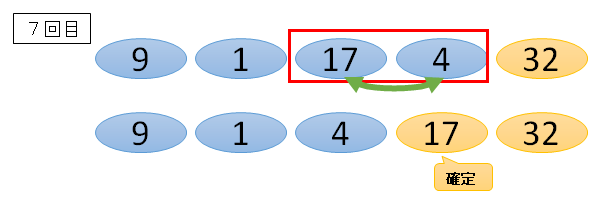
末尾の数字を確定させた時と同じように、3番目(上の図だと7回目の”17″)4番目(上の図だと7回目の”4″)と比較してあげれば、どちらかが4番目の数字として確定します。
今回は、17と4を入れ替えているので、17が4番目の数字として確定します。
3番目の数字の確定
次に、3番目の数字を確定させるために、先頭から順番に、3番目まで並び替えを行います。
(「もう理解したよ」っていう人は飛ばしてもらって大丈夫です 笑)
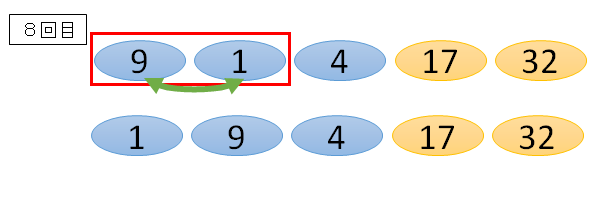
■先頭と2番目の数字
9と1だと、9の方が大きいので、右に並び替えます。
■2番目と3番目の数字
9と4だと、4の方が大きいので、右に並び替えます。
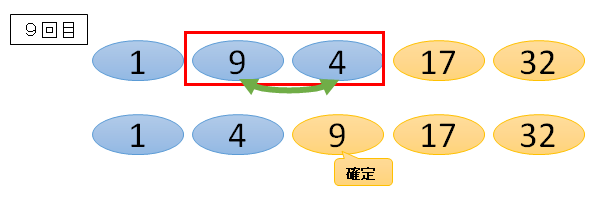
2番目(上の図だと9回目の”9″)3番目(上の図だと9回目の”4″)と比較してあげれば、どちらかが3番目の数字として確定します。
9と4を入れ替えているので、9が3番目の最大値として確定します。
2番目の数字の確定(ここで全部確定)
次に、2番目の数字を確定させるために、先頭と2番目の数字の並び替えを行います。
■先頭と2番目の数字
1と4は、4の方が大きいので、並び替えせず、そのままです。
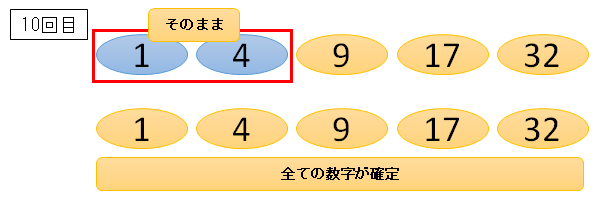
今回、先頭の数字の1と、2番目の数字の4を並び替えなかったので、2番目の数字は4で確定。
2番目~末尾の数字すべてが確定しているので、先頭の数字も1で確定です。
合計で、10回のソートを行い、きちんと、並び替えられています。
バブルソートの比較回数・計算量
バブルソートの比較回数と計算量(計算にかかる時間)を、さらっと書いておきます(基本情報をうけるだけなら、特に知る必要なし)。
- 【比較回数】n(n-1)/2
- 【計算量(最悪時間計算量)】O(n^2)
比較回数
比較回数は、データ数 n とすると、下記の通り。
(n-1)+(n-2)+・・・+1
初項n-1、末項1、項数n-1の等差数列の和(平均をもとめるのと同じ式)なので
{(n-1)+1}×(n-1)/2=n(n-1)/2
計算量
バブルソートの計算量(最悪時間計算量)は、多重ループするので、O(n^2)です。
※比較回数がn(n-1)/2=(n^2-n)/2で、2乗が出てくる=多重ループである
今回のように、5つくらいなら特に問題ないけど。
「1000あるデータをならびかえましょう!」みたいにデータが多いときは、別のアプローチが必要です。
バブルソートの他に覚えておきたい並び替えのアルゴリズム
バブルソートの他にも、いろんなデータの並び替えのアルゴリズムがあるので、覚えておくとよきです(*´ω`)。
- 【選択ソート(基本選択法)】最小値を選んで先頭に持っていくのを繰り返す
- 【挿入ソート(基本挿入法)】整列済みの列を増やしていって未整列の値を挿入
- 【シェルソート】一定間隔おきに取り出した値の列を並び替えて元に戻す
- 【クイックソート】基準値を決めて大小のグループに振り分けて並び替え
- 【ヒープソート】ツリー構造をつくって親と子の大小比較する
まとめ
バブルソートときたら、となり合うデータの大小を比較して並び替えること。
基本情報のアルゴリズムで、「バブルソート」って単語が出てきたときも。
まったく知らないのと、「大小を比較して並び替える」っていうのを知っているのとでは、問題文の読みやすさ・解くスピードが変わってくるので、おぼえたってください(-_-;)。

コメント