論理積（AND）とは？「AかつB」を表す

論理積（AND）は、「AかつB」を表します。

真である(正しい)場合を1、偽である(正しくない)場合を0とした場合、論理「積」なので、AとBの両方が正しければ、1×1=1となり、真(1)。

どちらかが正しくない場合は、AとBのどちらかが0となるので、かけ算の結果、偽(0)を返します。

論理積（AND）とは？

論理積（AND）は、「AかつB」のこと。すんなり来なければ、「AとBの両方が正しい場合」です。

ベン図とは？

ベン図について、高校数学のおさらいもかねてさらっと（知ってる人は飛ばしてね）。

ベン図は、集合（グループとかデータ）を表した図です。

例えば、「1から100までの数字」みたいなのが全体集合。集合A：「3の倍数」、集合B：「4の倍数」みたいなのを図にします。

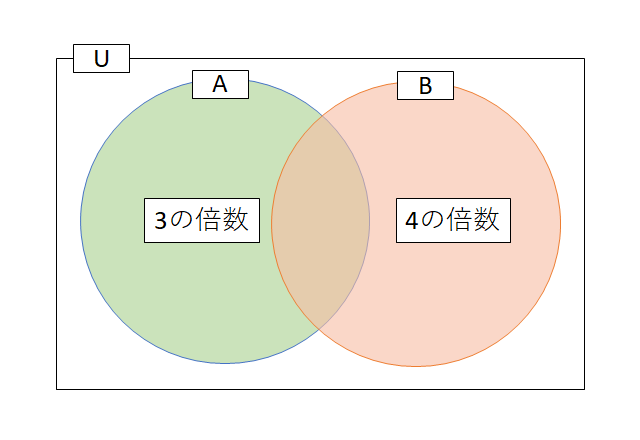
全体の集合と集合Aと集合Bを、「ひとまず書いてみようぜ」みたいなのがベン図です。

論理積（AND）とは、ベン図で交わっている部分、「かつ」を表す

論理積（AND）とは、ベン図で交わっている部分、「かつ」を表します。

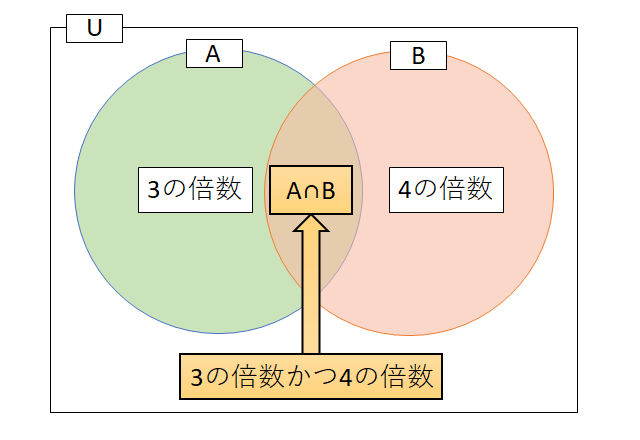
例えば、「1から100までの数字」があって、集合A：「3の倍数」、集合B：「4の倍数」のとき。

「AかつB」は、「3の倍数かつ4の倍数」ということになります。

「AかつB」であれば1（真）、それ以外は0（偽）

論理積（AND）では、「AかつB」、つまりAとBの両方が正しければ(真であれば)、真(1)。

どちらかが正しくなければ、偽(0)を返します。

A	B	AかつB	考え方
1	1	0	1×1=1
1	0	1	1×0=0
0	1	0	0×1=0
0	0	0	0×0=0

ついでに覚えておきたい論理演算

ついでに覚えておきたい論理演算も書いておきます。

論理演算	意味
論理積	AかつB
論理和	AまたはB
否定	Aでない
排他的論理和	Aだけ、もしくはBだけ

残念ながら、「論理積」という単語は、どちらかといえば前提知識。

これがわからないと、基本情報技術者試験でよく出る「論理回路」の話が、わけわかんなくなります(*´▽｀*)。

まとめ

論理積（AND）ときたら、「AかつB」のこと。

「論理『積』なので、AとBの両方が正しければ、1×1=1となり、真(1)になるんだな～」くらいに思っておいてください(-_-;)。