排他的論理和（XOR）とは？自分だけが真（1）であること

排他的論理和（XOR）とは、「自分だけが真（1）」であることです。

「排他」とは、自分以外をしりぞけるということ。よそ者をよせつけません。

真である(正しい)場合を1、偽である(正しくない)場合を0とした場合。

「排他的論理和」では、AとBがあるときに、自分「だけ」が1であれば、1になります。

どちらも正しくない(0である)場合、どちらも正しい(1である)場合は、0になります。

排他的論理和（XOR）とは、自分だけが真（1）であること

排他的論理和（XOR）とは、自分だけが1（真）であることです。

排他的論理和（XOR）をベン図で書く

排他的論理和（XOR）をベン図で書くと、下記の通り。

例えば、「1から100までの数字」みたいなのが全体集合。

集合A：「3の倍数」、集合B：「4の倍数」であるときの、排他的論理和は下記の通り。

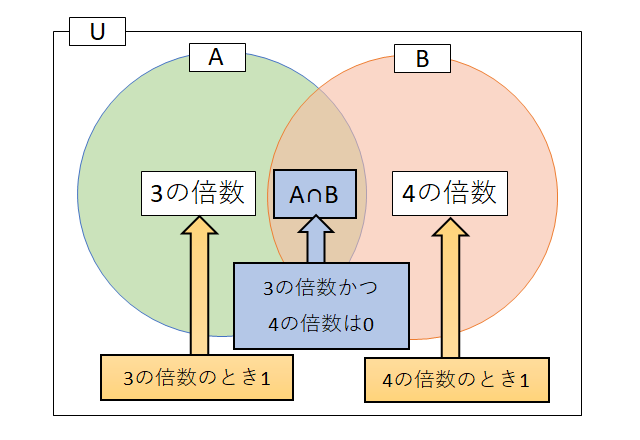
「Aだけ」・「Bだけ」であれば1（真）、それ以外は0（偽）

排他的論理和（XOR）では、「Aだけ」・「Bだけ」であれば1（真）、それ以外は0（偽）です。

A	B	排他的論理和(XOR)	考え方
1	1	0	AかつB
1	0	1	Aだけ
0	1	1	Bだけ
0	0	0	AでもBでもない

基本情報技術者試験のビット演算で排他的論理和をとる問題が出る

基本情報技術者試験のビット演算で排他的論理和をとる問題が、少なくとも3回に1回は出ます。

8ビットの値の全ビットを反転する操作はどれか。

ア　16進表記 00 のビット列と排他的論理和をとる。
イ　16進表記 00 のビット列と論理和をとる。
ウ　16進表記 FF のビット列と排他的論理和をとる。
エ　16進表記 FF のビット列と論理和をとる。

「令和元年秋期午前問2」より引用

【余談】16進数を2進数に変換

16進数で00は、値がゼロなので、00000000

16進数でFFを10進数に変換すると、16×15+15=255

255を2進数に変換すると、11111111

※16進数のFは15だから、FF=15×15
※2進数の変換は、わり算で地道にやってもいいけど、めんどうだからフィーリングです 笑
※16進数→10進数→2進数への変換は、言語化できたら書くね(*´▽｀*)。

【255の2進数を求めるフィーリング】
2の8乗は256、2の7乗は128なので、255は2の0乗から2の7乗の和である。
→2の7乗+2の6乗+・・・+2の0乗
→128+64+32+16+8+4+2+1=255
→11111111が求める2進数

【さらに余談】
225みたいな中途半端な数の場合は、うまいこと調整する。
128+64+32+16+8+4+2+1=255
から30を引けばいい。ちょうど、16+8+4+2=30となるのでこれを0にすれば225の完成。
→11100001が求める2進数

【まじめな解説記事】全ビットを反転する方法は？

ア：16進表記 00 のビット列と排他的論理和をとる

16進表記 00 のビット列と排他的論理和をとってみます。

てきとうに値は、01010101としてみます。

準備はいいですか？排他的論理和は、どっちか片方だけが1のときだけ、1。それ以外は、0です。

もと：01010101
ア　：00000000
——————-
排他：01010101

・・・元の数字と変わらないですね(*´ω｀)。

イとエ：論理和をとる→論外

イとエの「論理和をとる」は、書くまでもなく論外です。

論理和は、「どちらか片方でも1なら1、両方とも0なら0」です。

つまり、0→1になることはあれど、1→0になることはなく、0→1の一方通行です。

ウ：16進表記 FF のビット列と排他的論理和をとる

16進表記 FF のビット列と排他的論理和をとってみます。

くどいけど、排他的論理和は、どっちか片方だけが1のときだけ、1。それ以外は、0です。

エ　：11111111
もと：01010101
——————-
排他：10101010

お、見事に反転されましたね♪2進数のオール1との排他的論理和をとれば、ビット列は反転。これが正解です。

まとめ

排他的論理和（XOR）ときたら、「自分だけが真（1）」であること。

「『排他的』なので、AとBの両方が正しいのは許さない。Aだけが1なら1、Bだけが1なら1になるんだな～」くらいに思っておいてください(-_-;)。