「ヘソ賞球1個のパチンコ台(とあるとか、エヴァ 未来への咆哮)が、 ヘソ賞球3個の台より勝てないのか?」
といえば、「【理屈の上では】変わらない」が結論です。
ただ、今はどのパチンコ屋さんも、釘は鬼締めなのでね(*´ω`)。
必要以上に釘を閉めるのであれば、ヘソ賞球1個の方がお金が減るスピードが速くなるし、ネガティブになるのも無理はないかと。ひよこSEも、結果的には、1個返しは辛くなっていると思います。
ただ、賞球が1個,2個,3個,4個のどれであろうが、「ボーダー以上に回るか?回らないか?」の世界でしかないです。
理屈の上ではヘソ賞球1個の台が3個の台より勝てないわけではない
もう一度だけ言うと、ヘソ賞球1個だから勝てないというわけではありません。「【理屈の上では】変わらない」です。
ボーダー回転数以上回るか?の話でしかないから賞球は関係ない
パチンコは、「ボーダー回転数以上回るか?」の話でしかないので、賞球は関係ないです。
かなりざっくりと書くと・・・
- 【パチンコ台A】賞球3個で1Kあたりのボーダーが、20
- 【パチンコ台B】賞球1個で1Kあたりのボーダーが、18
の2台があったとして。
パチンコ台Aが1K(1000円)で、19回転しか回らないのであれば、ボーダーより1回転少ないので、れっきとしたマイナス調整。
パチンコ台Bが1K(1000円)で、19回転回ってくれるのであれば、ボーダーより1回転多く回るので、減りが早かろうがプラス調整。
シンプルにこれだけの話です。
「ヘソ賞球に関係なく、ボーダー以上回ればプラス。回らなければマイナス」と言うことに。エヴァ15のボーダーであれば、17回転/1K前後です。
現実はパチンコ屋さんが釘を閉めるので、結果的に賞球1個が辛い

そんなこと言ったって、返しが1だと、めっちゃ負けるよね?
その通りです。パチンコ屋さんが釘を閉めたら、賞球1個は激辛になります。
言ってしまえば、それ以上でもそれ以下でもないのだけど。
ここで終わっても面白くないので。
賞球1個と3個の出玉性能のちがいについて、もう少し踏み込んでいくので、興味がある人は、続きを読んでくれたらと思います。
1/319.7(ハイミドル)で、賞球1個は賞球3個より639.4玉だけ多く出せる
「ヘソの賞球が1個と3個では、そもそも出玉性能にどれだけ差があるのか?」
について、見ていきます。
現行のハイミドル(1/319.7)では、平均すれば319.7回転に1回、大当たりします(ホントかよは別にして)。
いいかえると、大当たりするまでに、ヘソに319.7回、玉が入るので・・・。
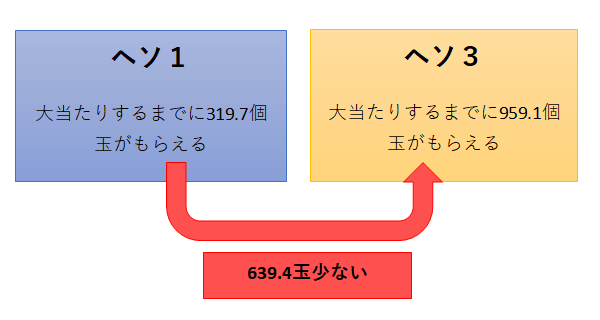
- 【ヘソ賞球1個の場合】319.7×1=319.7玉(①)
- 【ヘソ賞球3個の場合】319.7×3=959.1玉(②)
- 【もらえる玉数の差】②ー①=959.1ー319.7=639.4玉
639.4玉だけ、大当たりするまでにヘソからもらえる玉の数に、差があることになります。
ヘソ賞球1と3の出玉差(639.4個)の行方は大当たり出玉か一般入賞口
賞球1と3で、大当たりするまでの出玉差は、639.4個。
この「639.4個」の行方は、次のうちいずれかになります。
- 大当たり出玉に割り当てられる
- 一般入賞口に割り当てられる
大当たり出玉に全振りした場合

ここからはひよこSEの想像の世界になることについて、ご了承ください。
ヘソ賞球3個のボーダー19.98=ヘソ賞球1個のボーダー17.23
※ヘソの出玉差を大当たり出玉に全振りをした場合に限る
ユーザーからすれば、これが一番平和かつ、わかりやすいですよね(´▽`*)。
639.4個の差を、そのまま大当たり出玉にしてくれたら、「ヘソ賞球1個は辛い」というお話にそもそもならないので。

仮にこうなるとしたら、初当たりのヘソ出玉も増えそうだし、いいことしかない!
一般入賞口に割り振られる場合
ただ、現実的に考えれば、お察しのとおりです。
ヘソ賞球による出玉差が、そっくりそのまま大当たり出玉に割り振られることは、まずないです汗。

それじゃあ、639.4個の出玉はどこに行くの?

その逃げ道(?)として用意されているのが、一般入賞口。おまけポケットです。
ヘソ賞球1の台で、一般入賞口の賞球数が多めに設定されていたとしても。一般入賞口を締めるか締めないかは、完全にブラックボックスの世界(ひとことで言えば、「お店による」)ですね。
釘が締まれば、ヘソ賞球1はやはり辛い
ここからは、さらに想像の世界になります。
例えば、ヘソ賞球1個の台が作られたとして。
- ヘソ賞球1個だけど、3個の台より、320玉だけ大当たり出玉を多くしてあるよ!
- 残りは、一般入賞口を甘くしてね!良心にお任せするね!
みたいなのが、メーカーからパチンコ屋さん向けに送られているはずです。

「台の出玉性能の説明書的なものはある」と考えるのが普通かと。
さて、このとき。もう見飽きた数字かもですが、「639.4個だけ、甘くできる」のでしたね。
そのうちのいくつか大当たり出玉に。残りは、「本当に一般入賞口が甘くなるのか?」
ここまで書けば・・・。まぁ、わかると思います笑。
ほとんどの場合で、
一般入賞口が締められる
↓
ボーダー以上は回らない
↓
ヘソ1個で締められると、お金の減りも早い
となってしまいます。
結果的には、ヘソ賞球1個はヘソ賞球3個よりも辛くなってしまいます。
まとめ:ヘソ賞球1個の台の扱いは、優良店かを見分けるポイント
さて、これまでのお話を、期待値の観点から書いたのですが、ある程度は当たっていそうです。
やはり、一般入賞口に割り当てられるみたいですね。
というわけで結論を最後にまとめて終わります。
- ヘソ賞球の数で勝てる/勝てないは、「【理屈の上では】変わらない」
- 「ボーダー以上に回るか回らないか?」のお話でしかない
- 基本的には、ヘソの賞球の差だけ、大当たり出玉も多いはず
- 一般入賞口にも割り当てるなら、お店が釘を締めなければ解決する
- 一般入賞口に割り当てないなら、ヘソ1のお金の減りが早くなるので、辛いという感覚は正しい

コメント